第07讲 对CAPM的讨论

• CAPM说的是, 如果所有投资者都采用均值-方差分析来确定其最优组合, 那么在理想状态下(一致预期、无摩擦), 均衡时不同资产的期望回报率之间会具有一种线性关系—证券市场线, 即 越高的资产期望回报率越高, 越低的资产期望回报率越低, 如下所示

  $$E(r_i) - r_f = \beta_i[E(r_M) - r_f] = \frac{\sigma_{iM}}{\sigma_M^2} [E(r_M) - r_f]$$

• CAPM带来的收获远不止于这个定价方程, 更加重要的是, 在CAPM中得到的很多结论在后文的其他定价模型中也成立, 其带来的洞察在未来金融分析中会一直出现

7.1 从CAPM的视角看风险

7.1.1 风险与分散化

• 风险是金融分析的核心课题, 是判断资产是”好”是”坏”的最主要考虑因素, 当然也是资产期望回报率(同时也是资产价格)最重要的决定因素

• 马科维茨均值-方差分析的一个重要理念是”有得必有失”

  投资者既偏好高投资回报, 又厌恶投资中的风险, 因而会在二者之间做权衡

  但这并不意味着波动率高的资产需要提供更高的期望回报率来补偿投资者

• 决定资产期望回报率的不是资产回报率的波动率, 而是资产回报率于市场组合波动的相关性

  之所以会有这样反直觉的结论, 关键在于对风险的定义: 风险是对未来回报不确定性的度量

  但在资产定价的时候, 必须把投资者对不确定性的应对也考虑进来: 如果某些不确定性可以通过投资者自己的处理而被消除, 它就不应该算作真正的风险, 市场也就不应该对持有这些不确定性给出奖励

  均值-方差分析的核心逻辑是通过恰当地构造由多种风险资产形成的资产组合, 将自己的财富分散投资到组合中的各种资产上, 投资者可以将资产汇报中的一部分不确定性(波动率)消除掉: 分散化可以消除资产回报率中的一部分不确定性, 从而降低投资者需要承担的不确定性, 所以在金融学中讨论风险时, 永远要把风险和分散化联系起来分析, 只有那些无法通过分散投资消除掉的不确定性才是真正的风险, 才是需要在期望回报率中加以补偿的坏东西

• 无法通过分散投资消除掉的不确定性是什么?分散投资的极致是什么?

  答案很简单: 持有所有资产, 就做到了分散投资

  而所有资产合起来, 就是市场组合; 市场组合的波动率就是不能被分散的不确定性, 是资产定价时需要加以补偿的风险

• 从市场组合的波动率又怎么能跳到单一资产的风险和定价呢?

  市场组合是由所有资产组合起来的, 市场组合的波动率来自组合中所有资产的波动率, 但不同资产对市场组合波动率的贡献不一样

  对每一种资产来说, 只有那些与市场组合波动率正相关的波动才贡献了市场组合的波动率, 剩余的不相关部分则可被分散化消除小

  因此, 任意一种资产所包含的真正风险就由其波动与市场组合波动的相关性 来衡量, 因此完全可能发生的情况是, 一种资产回报率的波动率很大, 但它所包含的风险其实很小

  在文献中, 一般把市场组合所包含的不可通过分散化而加以消除的波动叫作系统性风险, 而各类资产所包含的可以通过分散化消除的波动叫作个体风险, 用这样的术语, CAPM可以概括为资产价格只奖励对系统性风险的持有

7.1.2 三个反直觉的问题

• 第一个问题: 假设一个药品研发公司和一家钢铁公司有相同的期望红利支付, 但药品研发公司红利支付的波动率更大, 问题是这两家公司中哪一家当前的股票价格应该更高

  没有学习CAPM之前, 我们可能会说, 因为药品研发公司红利支付的波动更大, 风险更高, 所以它更不受投资者欢迎, 因而需要给出更高的期望回报率来吸引投资者, 所以药品研发公司当前的股价应该耕地

  但是这是基于对风险的错误认识而得出的错误结论, 市场组合可以被认为反映了整个宏观经济的走势, 钢铁公司的经营状况显然与宏观经济有更高的相关性, 因而会与市场组合的波动有很高相关性( 高), 而药品研发虽然不确定性很大, 但它的波动应该与宏观经济没太大关系( 低)

  从CAPM关于风险的真正定义来看, 钢铁公司的风险高于药品研发公司, 所以钢铁公司当前的股价会低于药品研发公司, 以便给投资者提供更高的期望回报率作为补偿

• 第二个问题: 有没有可能存在期望回报率低于无风险利率的风险资产?

  当我们说一项资产是风险资产时, 这项资产的回报率显然会有波动, 如果仅仅把波动理解为风险, 那就会很容易认为不可能有期望回报率低于无风险资产的风险资产, 因为这样的资产看上去在期望回报率和风险两个维度上都劣于无风险资产, 自然不会有人愿意持有它

  但是, 回报率的波动未必是个”坏东西”: 如果这个波动与市场组合的波动正相关, 那它确实增加了资产持有者面临的风险, 但如果这个波动与市场组合的波动负相关, 那它反而可以对冲掉其他资产带来的一部分风险, 此时, 回报率的波动就变成了一个”好东西”, 投资者会愿意牺牲一点期望回报率来持有它, 所以, 期望回报率低于无风险利率的风险资产是完全可能存在的

• 第三个问题: 面对两种期望回报率一样的资产, 投资者是否一定会选择波动率小的资产而不选择波动率大的?类似可问, 面对两种波动率一样的资产, 投资者是否一定会选择期望回报率高的而不选择期望回报率低的?

  回答是: 是, 又不是

  先说”是”这一部分, 从均值-方差偏好来看, 答案显然应该是肯定的, 再展示以下第六章推导CAPM定价方程时使用过的效用函数:

  $$u(r) = E(r) - A\sigma^2(r)$$

  从这个效用函数来看, 如果两种资产的波动率相等, 那一定是期望回报率高的资产能带来更高的效用, 又因为A是个大于0的数(人都是风险厌恶的), 所以两种回报率一样的资产, 一定是波动率小的资产带来更高的效用

  再来说”不是”的这一部分, 当投资者面对两种期望回报率一样而波动率不一样的资产时, 投资者并非是在做二选一的选择题, 完全有可能的是, 将波动率高的资产加入投资者的组合中, 反而会改善整个组合的回报和风险特征(获得更高的夏普比), 因而投资者也会愿意持有波动率高的资产

  事实上, 正如在均值-方差分析和CAPM种所看到的那样, 市场上所有资产(不管其回报率和波动率是怎样的)都会被投资者持有

  这两个回答并不矛盾, 关键是两个资产各自的方差并不是进入效用函数的方差, 投资者在计算自己的效用时, 一定是以最优组合的方式持有了所有资产之后, 再计算自己的效用, 所以, 在这个效用函数中的方差只能是投资者持有的最优资产组合的方差, 而不是各个资产自身回报率的方差

  均值-方差偏好只能用来做评价最优组合的判断标准, 在这些最优组合种, 所有可被分散的风险都已被分散, 只存在系统性风险, 在这些最优组合中, 如果两个组合期望回报率一样, 而波动率又不同, 那么投资者一定会选择波动率小的那个最优组合, 而对任意(风险未被充分分散)两种资产, 不能用均值-方差偏好来说投资者会选择一个, 而不选择另一个

7.1.3 一个例子

假设又两个聚宝盆A和B, 所有投资者只能选择这两种风险资产, 明天, 有1/2可能性聚宝盆A里出现1元钱, 同时B里什么也没有; 还有1/2的可能性聚宝盆B里出现1元钱, 同时A里什么也没有; 假设今天到明天的无风险利率为0—今天借1元, 明天还1元, 那么聚宝盆A和B在今天的价格分别为多少?

很容易计算出两个聚宝盆的期望回报和方差:

$$\begin{aligned} E(A) = E(B) &= 0.5\times 1 + 0.5 \times 0 = 0.5\\ var(A) = var(B) &= 0.5\times (1 - 0.5)^2 + 0.5 \times (0 - 0.5)^2 = 0.25 \end{aligned}$$

这并不意味着为了吸引人在今天持有聚宝盆A, 聚宝盆A今天的价格应该小于它明天的期望回报0.5, 从而令持有聚宝盆的期望回报率大于0这个无风险利率

要以资产组合的思路来审视这个问题, 由于只存在A和B两种风险资产, 所以包含所有风险的市场组合M也就只可能包含这两种资产

假设某个组合 是由 份额的聚宝盆A, 以及 份额的聚宝盆B所组成, 则 明天的期望回报为

$$E(P_w) = 0.5 \times w + 0.5 \times (1-w) = 0.5$$

而组合回报的方差为

$$\begin{aligned} var(P_w) &= w^2var(A) + (1-w)^2var(B) + 2w(1-w)cov(A,B)\\ &= 0.25w^2 + 0.25(1-w)^2 + 2 w(1-w) [E(AB) - E(A)E(B)]\\ &= 0.25w^2 + 0.25(1-w)^2 + 2 w(1-w) (0 - 0.25)\\ &= 0.25[w^2 + (1-w)^2 + 2w^2 - 2w]\\ &= 0.25(4w^2 - 4w +1)\\ &= 0.25 (2w-1)^2 \end{aligned}$$

显然当 时, 组合回报的方差为0, 也就是说, 持有1/2个聚宝盆A和1/2个聚宝盆B的组合变成一个无风险的资产, 明天的回报确定性地为0.5, 所以这个组合地回报率应该就是无风险利率, 相应的, 这个组合在今天的价格一定为0.5, 组合 一定就是市场组合M, 只不过这时情况很特殊, 市场组合就是无风险资产, 而市场组合与聚宝盆A或B的回报的协方差均为0, 所以A和B的 均为0, 因此, 根据CAPM, A和B的回报率都不含有风险溢价, 应该等于无风险利率0, 相应的, A和B今天的价格都应该等于它们明天的期望回报, 也就是0.5, 如果低于0.5, 那就出现了套利机会, 均衡时, A和B的价格一定等于0.5

在这个例子中, 可以看出回报(率)本身的波动并不一定导致市场的风险补偿, 也就是说, 市场并不会因为投资者承担了波动, 就提供风险溢价, 对于可以消除的波动, 市场就不会给予补偿

用CAPM的框架来看, 无风险利率 一定是0, 但 是0的资产一定是无风险资产吗? 未必, 在这个例子中, 可以看到聚宝盆A和B的 都应该是0, 但它们单独来看都不是无风险的, 为0的资产只是期望回报率应该等于无风险利率, 但未必是无风险资产

7.2 CAPM的估计

前文已经推导出了CAPM定价方程—证券市场线SML, 这是用真实数据来检验的数量关系, 因此对CAPM的估计就从这个直线方程入手

定义某资产 的超额回报率(回报率减去无风险利率)为 , 市场组合M的超额回报率为 , 根据SML的公式有如下公式成立

$$E(\tilde{r}_i) = \beta_i E(\tilde{r}_M)$$

由于真实世界中还会有其他因素也在影响资产期望回报率, 所以当用真实世界中的数据来检验时, 上式应该不会那么精确地成立, 因此在实践中, 估计CAPM的计量模型采取如下形式

$$\tilde{r}_i = \alpha_i + \beta_i \tilde{r}_M + \tilde{\varepsilon}_i$$

上式又被称为单一指数模型, 截距项和残差项都代表了资产回报率中不能为市场组合所解释的部分, 如果CAPM理论精确成立, 市场只补偿资产所含有的系统性风险, 而不补偿资产中的个体风险, 那么 与 都应该是0, 但现实中往往不是这样

可以用最小二乘法(OLS)来估计上式的计量模型, 第 期某资产 和市场组合的超额回报率分别记为 与 , 所谓市场组合, 理论上是包含所有资产的资产市场—除股票、债券等常见证券外, 甚至包含房地产、人力资本等交易没那么活跃或是干脆无法交易的资产, 显然这种严格意义下市场组合的回报率是无法获得的, 所以在实践中, 往往用股票市场的总指数来代表市场组合, 由于股票指数的波动远远大于其他资产价格的波动, 市场组合的波动应该接近股票指数的波动, 因此, 用股票指数来代表市场组合也算一个不太差的近似

如果已经知道了 和 的取值, 那么在每一个时期 都可以计算出一个残差:

$$\varepsilon_{it} = r_{it} - \alpha_i - \beta_ir_{Mt}$$

OLS估计就是要通过选取 和 的取值来使得各期的残差平方和最小, 如下所示:

$$\min_{\alpha_i, \beta_i} \sum_{t=0}^T \varepsilon^2_{it} = \sum_{t=0}^T (r_{it} - \alpha_i - \beta_ir_{Mt})^2$$

通过OLS得到的 的估计值是

$$\hat{\beta}_i = \frac{cov(\tilde{r}_i, \tilde{r}_M)}{var(\tilde{r}_M)} = \frac{\sigma_{iM}}{\sigma_M^2}$$

也就是说, 估计出来的 应该等于资产 的 , 这就给出了一种计量方法找出每种资产 的方法

按定义应该是不能被 解释的部分, 从而有

$$cov(\beta_i\tilde{r}_M, \tilde{\varepsilon}_i) = 0$$

所以

$$\begin{aligned} var(\tilde{r}_i) &= var(\alpha_i + \beta_i \tilde{r}_M + \tilde{\varepsilon}_i)\\ &=var(\beta_i \tilde{r}_M) + var(\tilde{\varepsilon}_i) + 2cov(\beta_i\tilde{r}_M, \tilde{\varepsilon}_i)\\ &= \beta_i^2var(\tilde{r}_M) + var(\tilde{\varepsilon}_i)\\ &= \beta_i^2 \sigma_M^2 + \sigma^2_{\varepsilon_i} \end{aligned}$$

因为无风险利率被认为是个常数, 所以资产 的超额回报率 () 的波动就是资产 回报率的波动; 在资产 回报率的方差中, 叫作系统性方差, 叫作个体风险, 它们就是系统性风险和个体风险的具体表征; 而在金融业中, 往往用 来简单指代市场中的系统性风险

7.3 CAPM的应用

7.3.1 运用CAPM确定贴现率

有了CAPM模型, 就可以来回答在股票价值分析中提出的问题: 贴现风险现金流时, 改用什么样的贴现率? 对于一个现金流不确定的项目, 可以用它过去回报率的历史数据计算这一项目的 , 进而用CAPM定价方程来对这个项目而言合理的贴现率

例如, 假设用戈登模型来估计一只股票的价格, 已知这只股票下一期的分红为10元, 未来红利增长预期为10\%, 这个公司的 , 无风险利率为5\%, 市场组合的风险溢价为 10\%, 于是可以知道这个公司的恰当贴现率应该是 , 这样, 按照戈登模型, 这只股票的价格就应该是 元

7.3.2 运用CAPM来简化投资组合优化问题

用均值-方差分析来做组合优化时, 需要知道所有资产(假设有 种)的回报率均值、回报率方差, 以及两两之间的回报率协方差, 可以写成如下形式:

$$\bar{r} = \begin{bmatrix} \bar{r}_1 \\ \bar{r}_2 \\ \vdots \\ \bar{r}_N \end{bmatrix} \hspace{3em} \sum = \begin{bmatrix} \sigma_1^2 & \sigma_{12} & \cdots & \sigma_{1N} \\ \sigma_{21} & \sigma_{2}^2 & \cdots & \sigma_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{N1} & \sigma_{N2} & \cdots & \sigma_{N}^2 \\ \end{bmatrix}$$

种资产的均值共有 个, 而由于 种资产形成的方差-协方差矩阵 是一个对称方阵, 所以其中共有 个独立的元素, 这样, 为了进行组合优化的计算, 总共需要估计 个指标, 在 很大的时候, 估计工作会非常艰巨

运用CAPM, 可以大大减少需要估计的参数的数量, 前文说过两种资产回报率之间的协方差等于二者超额回报率之间的协方差, 即

$$\sigma_{ij} = cov(r_i, r_j) = cov(\tilde{r}_i, \tilde{r}_j)$$

代入前文提到的计量模型:

$$\begin{aligned} \sigma_{ij} &= cov(\tilde{r}_i, \tilde{r}_j)\\ &= cov(\alpha_i + \beta_i \tilde{r}_M + \tilde{\varepsilon}_i, \alpha_j + \beta_j \tilde{r}_M + \tilde{\varepsilon}_j)\\ &= \beta_i \beta_j cov(\tilde{r}_M, \tilde{r}_M) + cov(\tilde{\varepsilon}_i, \tilde{\varepsilon}_j)\\ &= \beta_i \beta_j \sigma_M^2 \end{aligned}$$

这样就可以把 种资产的方差-协方差矩阵改写为

$$\sum = \sigma_M^2 \begin{bmatrix} \beta_1^2 & \beta_1 \beta_2 & \cdots & \beta_1 \beta_N \\ \beta_2 \beta_1 & \beta_{2}^2 & \cdots & \beta_2 \beta_N \\ \vdots & \vdots & \ddots & \vdots \\ \beta_N \beta_1 & \beta_N \beta_2 & \cdots & \beta_{N}^2 \\ \end{bmatrix}$$

于是, 去除市场组合的方差 外, 只需要估计 种资产的 个 就足够写出方差-协方差矩阵了, 做组合优化所需的参数数目就变成了 , 远小于

7.3.3 运用CAPM来衡量投资业绩

衡量一只投资基金的业绩主要有两个主要指标, 夏普率和詹森阿尔法, 后者就源自CAPM, 夏普比的定义前文提到过:

$$SR_i = \frac{\bar{r}_i - r_f}{\sigma_i}$$

它衡量了承担单位风险所获得的回报率提升的幅度, 由于其比较容易理解且容易计算, 所以被广泛使用

但是, 夏普比之应该被用来衡量那些被提供给最终投资者的资产组合的表现, 对单个资产计算夏普比的意义很小, 因为单个资产并未享受到分散化带来的好处, 其夏普比理应低于市场组合, 所以某个基金直接面向最终客户, 那么它就有义务通过分散投资将个体风险在组合中消除掉, 对这样的基金来说, 夏普比就是衡量其表现得一个不错指标

在现实世界中, 还有些基金只专注于投资某一个领域, 比如黄金、成长股、债券等的基金, 这些基金在设立之时就明确表示不会尽可能地做分散投资, 这些基金的客户(主要是投资领域广泛的基金)会在这些行业基金的基础之上, 再来构造自己的基金, 母基金(funds of funds, FOF) 就属于这一类基金

对于这些行业性或局域性的基金, 夏普比不是一个公允的指标, 因为这些行业性基金本来就不会尽可能分散投资, 对于这些基金来说, 而非波动率时更合适的风险刻画指标

1968年迈克尔·詹森利用CAPM的思想构造了一个衡量共同基金表现的指标—詹森阿尔法(简称Alpha), 这个指标又被称为詹森指数, 简单来说, 詹森阿尔法是某只共同基金平均回报率相对证券市场线的垂直偏离:

$$Alpha = (\bar{r}_i - r_f) - \beta_i(\bar{r}_M - r_f)$$

其实就是前文OLS回归方程的截距项 , 这是詹森阿尔法得名的由来

如果某只共同基金的Alpha为正, 即时这只基金的夏普比低于市场组合, 也应该判断这只基金的基金经理表现优异, 原因在于, 可以通过将Alpha为正的基金于市场组合再做组合, 得到夏普比该与市场组合的资产组合, 也就打败了市场

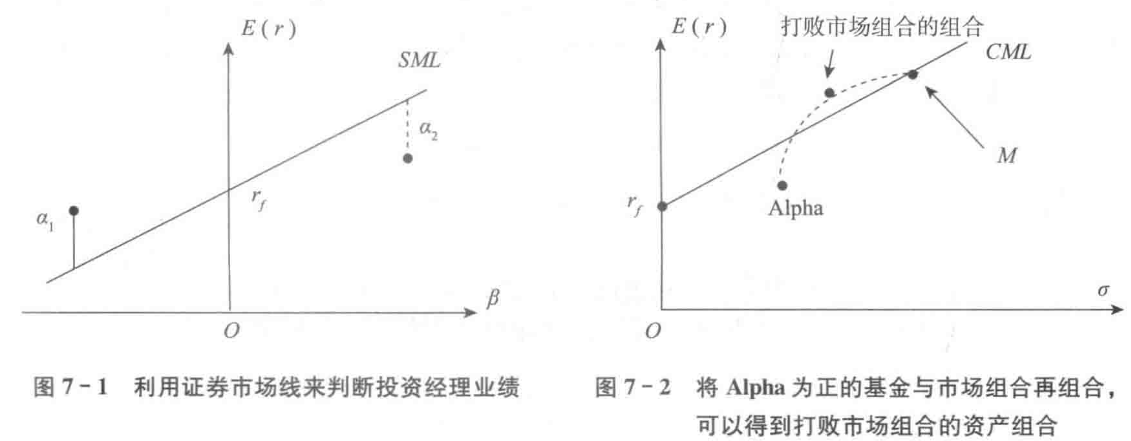
事实上, 均衡时所有资产(包括基金)的Alpha都为0, 如果有基金出现了正Alpha, 就表明市场没有处在均衡状态, 这时市场就会调整, 把这个正Alpha基金吸收到新的市场组合中, 从而得到比原来市场组合更高的夏普比

7.3.4 Alpha与Beta的分离

前文说过, 如果能够找到一个正Alpha的基金, 可以把这个基金与市场组合再组合, 得到比原来市场组合更高的夏普比, 在实践中其实并不那么复杂, 我们完全可以在组合构建种把这个正的Alpha提取出来, 这种策略叫作Alpha与Beta分离(alpha Beta separation), 这个分离出来的Alpha可以被加到其他组合中, 以帮助其他组合获得更高的回报率, 所以这种策略又叫作Alpha转移(Alpha transport), 或者叫可携Alpha(portable Alpha)

用一个例子来展示

• 假设一只基金A, 其规模为1亿元, 回报率 如下:

  $$r_A = r_f + 0.03 + 1.5(r_M - r_f) + \varepsilon$$

  可以看出, 这只基金的Alpha为0.03, Beta为1.5, 这只基金的Alpha为正可能是因为基金经理选股能力较强, 总能找出行业中表现好的股票

  为了把A基金中的Alpha分离出来, 我们构造一只对冲基金H, 基金H的规模也为1亿元, 基金H用无风险利率借入5000万元, 再加上自有的1亿元, 总共1.5亿元投资在市场组合上, 基金H的回报率应该为

  $$r_H = -0.5r_f + 1.5r_M = r_f + 1.5(r_M - r_f)$$

  由于基金H只投资于无风险资产(负头寸)和市场组合, 所以在其回报率公式中没有随机扰动项

  再构造一个新的组合 , 它包括1亿元A基金的多头, 1亿元H基金的空头(卖空H基金来买入A基金), 那么这个组合 的回报率应该是

  $$\begin{aligned} r_p &= r_A - r_H \\ &= r_f + 0.03 + 1.5(r_M - r_f) + \varepsilon - r_f - 1.5(r_M - r_f) \\ &= 0.03 + \varepsilon \end{aligned}$$

  如果A基金中的个体风险 比较小, 那么就能通过组合 来获得接近于0.03的回报率, 注意, 组合 的净规模为0, 这样就通过组合 获得了近乎无风险的0.03的回报率

  在实践中, Alpha带来的总回报可能不大, 但是基金公司可以把这些Alpha作为一个卖点, 来促进其他更大规模基金的销售, 把Alpha从原来的A基金中分离出来, 再转移给其他基金, 就是在做Alpha转移, 被分离出来的Alpha就是可携Alpha

  在实际操作中, 其实并不需要构建对冲基金H, 直接利用股指期货做对冲就行了, 股指期货可以被理解为对应市场组合的期货, 其Beta为1, 通过选择合适的股指期货头寸规模, 就能够对冲掉一个组合中的Beta风险, 而只留下Alpha

7.4 CAPM的不足

由于其理论和实践上的不足, CAPM只是均衡定价理论体系的起点, 其留下的各种问题称为后来定价理论发展的主要动力

理论上的不足:

• CAPM是一个均衡资产定价理论, 但它只是部分均衡的理论: CAPM只研究资产市场中的均衡, 而将资产市场所处的宏观环境当成外生给定

• CAPM还是一个静态模型, 之研究单期决策的问题, 难以把资产价格和宏观经济的各种因素联系起来, 无法探究资产价格的最终决定因素

• CAPM也无法分析资产价格的动态变化规律, 基于消费的资本资产定价模型(C-CAPM)和跨期资本资产定价模型(ICAPM)就是针对这两点不足发展出来的更成熟的定价理论

CAPM在实践中的不足也很明显:

在用数据估计CAPM所对应的单一指数模型时, 估计的结果很不理想

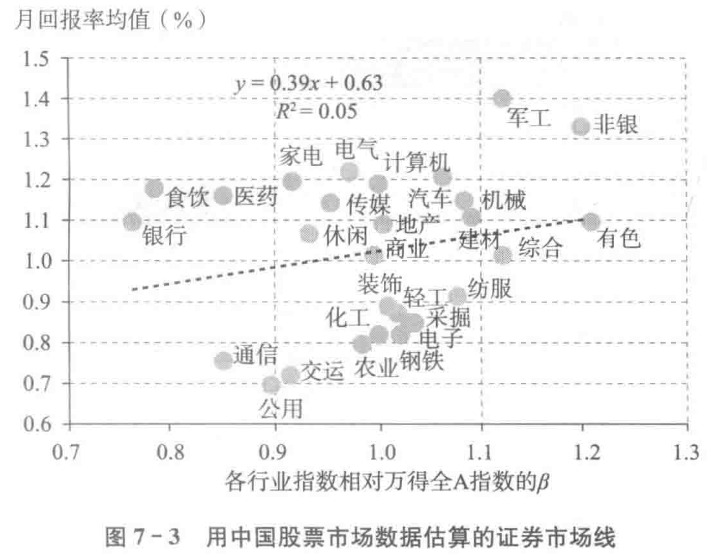
在上图中列出了用2001年1月到2017年2月我国A股市场月度数据估算的证券市场线, 市场组合用万得(Wind)全A指数表示, 股市中各个行业的股价则用申万一级行业指数来表示, 拟合优度 只有0.05, 低 行业的回报率有巨大的分化

对CAPM与现实的偏离的解释有几个角度:

• 验证CAPM时采用的市场组合不能完全代表真正的、完全分散了风险后的市场组合

• CAPM未能考虑到现实世界的复杂性, 比如税收政策、交易的限制等摩擦因素

• 除市场组合外, 可能还有一些其他因素(通胀水平、经济增速、股份公司规模大小等)也对股价有影响, 为了把这些其他因素也纳入定价理论的框架, 多因子模型也被开发出来

尽管有种种不足, 均值-方差分析与CAPM仍然提供了一个思考回报与风险的框架, 其蕴含的思想在其修正后的模型中得以继承与发扬, 从这个角度来说, CAPM是理解现代投资学的起点